c-study

C语言学习

建议：一定要多手打或者手写代码，不要只看书（因为这样难以应付幽默考试，而且记忆也不深刻

char就是int

为什么说char就是int？如果理解、分辨字符和整型之间的区别？

ASCII码把int和char联系到了一起，通过转义字符“ \ ”，搭起了桥梁。

字符：如 ‘a’, ‘1’ 等，都可以看作十进制的整型（具体值对应ASCII码中）。我们也可以

int str = '\10'; // 这里就的\10 就是八进制对应的字符，所以对应int的8；
int str = 'a' //那么 str储存的就是a对应的int。

总而言之，字符就是int。

typedef的另类使用

参考链接：C/C++ typedef用法详解（真的很详细）-CSDN博客 |

typedef中声明的类型在变量名的位置出现！！于是可以理解函数指针中的定义

typedef 是 C 语言中一个非常有用的关键字，它的主要作用是为现有的数据类型定义一个新的别名。通过 typedef，可以让代码更具可读性、简洁性和可维护性。以下是 typedef 在 C 语言中的常见运用场景及其详细说明：

typedef int Integer;
typedef float Real;

Integer age = 25;       // 等价于 int age = 25;
Real salary = 5000.50;  // 等价于 float salary = 5000.50;

typedef int* IntPtr;

IntPtr p1, p2;  // 等价于 int *p1, *p2;

typedef int Vector[10];  // 定义一个包含 10 个 int 元素的数组类型

Vector v;  // 等价于 int v[10];

// 定义结构体并为其定义别名
typedef struct {
    int x;
    int y;
} Point;

Point p1;  // 等价于 struct { int x; int y; } p1;

typedef int (*MathFunc)(int, int);  // 定义一个函数指针类型

int add(int a, int b) {
    return a + b;
}

int main() {
    MathFunc func = add;  // 使用别名声明函数指针
    printf("Result: %d\n", func(2, 3));  // 输出 5
    return 0;
}

typedef enum { RED, GREEN, BLUE } Color;

Color c = RED;  // 等价于 enum { RED, GREEN, BLUE } c = RED;

typedef struct {
    int year;
    int month;
    int day;
} Date;

typedef struct {
    char name[50];
    Date birthday;
} Person;

Person p1;  // 使用别名声明复杂结构体变量

---

#include<stdio.h>
int test(int a,int b)
{
    /*do something*/
    return 0
}
typedef int(*fp)(int,int);
int main(void)
{
    fp f1 = test; //表达式1
    fp f2 = &test;//表达式2
    printf("%p\n",f1);
    printf("%p\n",f2);
    return 0;
}

在这里，声明了返回类型为int，接受两个int类型参数的函数指针f1和f2，分别给它们进行了赋值。表达式1和表达式2在作用上并没有什么区别。因为函数名在被使用时总是由编译器把它转换为函数指针，而前面加上&不过显式的说明了这一点罢了。

---

动态内存分配malloc的再探索与形参实参的研究

参考链接：C语言visual studio警告：取消对NULL指针“p”的引用_取消对null指针的引用怎么解决-CSDN博客 |看完这篇文章一定弄懂C语言数组作为函数参数的用法_使用可变长度的数组作为函数参数-CSDN博客

形参和实参：malloc为例

tip: free指针后最好重置指针。

中午突然不明白C语言中的形参和实参在函数中的传递规律，由于free()的使用。

void clear_p(int* p) {
    free(p); 
    p = NULL; // 倘若 没有这一句，我们会发现
}

void fun(int* p)
{
    p[0] = p[1];
}

int main()
{
    int* p;
    int n =2；
    p = (int*)malloc(n * sizeof(int));
    if (!p) return 3;
    
    p[0] = 0;
    p[1] = 1;
    fun(p);
   printf("%d", p[0]);
   
   clear_p(p);
   printf("%d", p[0]);
   
    if (p != NULL) {
        return 1; }
    else if (p == NULL) {
        return 0; } 
}

经过上面的代码分析，我们可以发现，main 中return 1； printf的两个数分别为1 和 * ；这说明在clear_p中，free改变了传入的参数，而p = NULL并未影响传入的参数。这是为什么呢？？

首先，要明确C语言中的参数传递是值传递。当调用clear_p(p)时，传**递的是指针p的值，也就是内存地址的副本。**在函数内部，这个副本被free释放，但main中的p本身并没有被修改，仍然指向原来的地址，此时这个指针变成了悬垂指针（野指针），因为它指向的内存已经被释放。

但是，free操作本身是成功的，因为它释放的是指针所指向的内存块，而不管是通过原始指针还是副本指针。即使传递的是指针的副本，free函数会根据传入的地址来释放对应的内存。因此，main中的p所指向的内存确实被正确释放了。

不过，main中的p变量本身的值（即存储的地址）并没有改变，仍然指向已经被释放的内存区域。这就是为什么在之后检查p != NULL时，条件成立，返回1的原因，因为clear_p函数中的p = NULL只是修改了函数内部的副本，不影响main中的p。

自此，我也了解了函数中形参传递了

那，为何fun(int *p)也能改变p？？，因为我们在调用fun时，传入的参数p实际上是&p[0]，也就是地址。也就是说，形参拷贝了一份p[0]地址的副本，形参确实不会改变实参的值（即 p所指向的地址），但我们对其解引用（*p）时，还是对同一个地址操作，那自然会改变实参。

函数介绍：realloc

p = (int * ) realloc(p, (n * sizeof(int) ))

这里的realloc为重新分配内存，一般会比原来分配的要大。成功返回新地址，失败返回NULL。

注意，realloc会自动释放原有内存。所以不用free

函数指针

定义，这里定义了pf为一个指针，它指向一个返回类型为void，传入参数为char *的函数。

void (*pf) (char *)

简单使用

void fun1(char *);
void fun2(char *);
int rount();

void (*pf)(char *);
pf = fun1; //正确		pf = rount; // 错误
//下面调用
(*pf)(mis); //  等价于: fun1(mis)
pf(mis); //同上

把函数指针作为函数参数

void show(void (*fp)(char *), char *str);

show(fun1, mis);
show(fp, mis);

else

show(sqrt(4.0));意思是传入sqrt的返回值。
show(sqrt);//传入函数地址

使用示例

typedef int (*func)(ElemType, ElemType);
int f_compare(ElemType input, ElemType judge);
void LocateElem(func man);

int main()
{    
...
   func f1 = f_compare;
   LocateElem(f1);  
...
return 0;
}

字符函数

ctype.h

有  isblank() ; //是否为空格、tab。注意，如果为真，则返回一个非0值！！！！，所以如果写if(isblank(a) == TRUE) 是不可取的
	isdigit(); //数字
	等等等等。
	tolower() // 返回小写字母

memset

void *memset(void *str, int c, size_t n)

• str – 指向要填充的内存区域的指针。

• c – 要设置的值，通常是一个无符号字符。

• n – 要被设置为该值的字节数。

#include <stdio.h>
#include <string.h> // 引入 string.h 头文件以使用 memset

int main() {
    char buffer[10];

    // 将 buffer 数组的前5个字节设置为字符 'A'，并添加字符串终止符
    memset(buffer, 'A', 5);
    buffer[5] = '\0'; // 确保添加字符串终止符
    printf("Buffer after memset: %s\n", buffer);

    // 将 buffer 数组清零，使用 '\0' 替代 0
    memset(buffer, '\0', sizeof(buffer)); // 使用'\0'确保一致性及可读性
    printf("Buffer after memset: %s\n", buffer);

    return 0;
}

perror

C 库函数 void perror(const char \*str) 把一个描述性错误消息输出到标准错误 stderr。首先输出字符串 str，后跟一个冒号，然后是一个空格。

字符串函数

strtol——char *转换为long

定义在stdlib.h

long int strtol (const char* str, char** endptr, int base);

str为要转化的字符串；base为转化的进制数，为0时默认10进制，0x采用16进制，0采用8进制；endstr为第一个不能转换的字符指针，为NULL时表示不用这个参数。根据这个可以作连续转换

strtol() 会扫描参数 str 字符串，跳过前面的空白字符（例如空格，tab缩进等，可以通过 isspace() 函数来检测），直到遇上数字或正负符号才开始做转换，再遇到非数字或字符串结束时(’\0’)结束转换，并将结果返回。如果不能转换或者 str 为空字符串，那么返回 0(0L)；

char nm[] = "202 22 2 1 3";
char *p_end;
int li1 = strtol(nm, &p_end, 10); // 这里用int是因为win系统下，int long都占4字节
int li2 = strtol(p_end, &p_end, 10); //可以预见的是，li1为202，li2为22；
...

strtok——分割利器

定义在string.h中

char *strtok(char *str, const char *delim);

str：要分割的字符串，第一次调用时传入需要分割的字符串，之后传入 NULL。NULL表示：函数将在同⼀个字符串中被保存的位置开始，查找下⼀个标记。（如果字符串中不存在更多的标记，则返回 NULL 指针。）

delim：分隔符字符串，用于指定分隔字符串的分隔符集合。

strtok函数找到str中的下⼀个标记，并将其⽤ \0 结尾，返回⼀个指向这个标记的指针。

（注：strtok函数会改变被操作的字符串，所以在使⽤strtok函数切分的字符串⼀般都是临时拷贝的内容并且可修改。）

//示例
char arr[] = "[email protected]@.gaoerji";
    char* sep = "@."; // @  . 作为两个分割符
    char* str = NULL;
    // 使用 strtok 函数进行字符串分割，每次调用都会返回被分割出的部分
    for (str = strtok(arr, sep); str != NULL; str = strtok(NULL, sep)) //巧妙的利用最开始的参数只初始化一次的特性
    {
        // 输出每次分割得到的子字符串
        printf("%s\n", str);
    }

fgets——代替gets

定义在stdio.h中

char *fgets(char *str, int n, FILE *stream)

fgets会储存换行符（当然，如果你输入超过n，换行符会没地方储存），最大读取为n-1个字符；返回值为指向str的指针，若读取到文件结尾，返回NULL

第三个参数为读取的文件，这里用stdin从键盘读取，后续会在文件操作中介绍

while(fgets(words, 10, stdin) != NULL && word[0] != '\n')
{
	i = 0;
	while(words[i] != '\n' && words[i] != '\0')
	i++;
	if(words[i] == '\n')  // 如果先遇到换行符，换成空字符； 先遇到空字符，else便丢弃多的字符
	  words[i] == '\0';
	else
	while(getchar() != '\n')   //这个操作就是说，一直getchar，知道传入的是‘\n’
     	continue; //清除缓冲区
     puts(words); // 上面一番操作使得str一定没有换行符
}

fputs——puts

int fputs(const char *str, FILE *stream)

fputs不会在输入末尾添加换行符，puts会。第二个为要写入数据的文件（把str puts 到 FILE中），在屏幕上用stdout。

自定义s_gets输入函数

这个函数读取整行输入并用空字符代替换行符。读取n-1个字符，并丢弃剩下的。

char *s_gets(char * st, int n)
{
	char * ret_val;
	int i = 0;
	
	ret_val = fgets(st, n, stdin);
	if(ret_val)
	{
	while(st[i] != '\n' && st[i] != '\0')
	i++;
	if(st[i] == '\n') 
	  st[i] == '\0';
	else
	while(getchar() != '\n')  
     	continue; 
	}
	return ret_val;
}

sprintf——合成字符串

int sprintf(char *str, const char *format, ...)

sprinf(str, "%s, %d, %c", stri, 2, c);

strncat——拼接字符串

char *strncat(char *dest, const char *src, size_t n)

• dest – 指向目标数组，该数组包含了一个 C 字符串，且足够容纳追加后的字符串，包括额外的空字符。
• src – 要追加的字符串。
• n – 要追加的最大字符数。

strncpy——复制

char *strncpy(char *dest, const char *src, size_t n)

• dest – 指向用于存储复制内容的目标数组。
• src – 要复制的字符串。
• n – 要从源中复制的字符数。

   char src[40];
   char dest[12];
  
   memset(dest, '\0', sizeof(dest));
   strcpy(src, "This is runoob.com");
   strncpy(dest, src, 10);
//	desk 最终的目标字符串： This is ru 

strncmp——比较

int strncmp(const char *str1, const char *str2, size_t n)

比较前n个字符有么有相同的。

if(strncmp(list[i], "astro", 5) == 0)

strcmp

两个字符串相同则返回0

strlen

不计算空字符‘\0’

文件操作✨

1. 文件定义

参考链接：C语言文件操作超详解（万字解读，细致入微）-CSDN博客 |

FILE

一般都是通过一个FILE的指针来维护这个FILE结构的变量（通过FILE类型的指针找到文件信息区的起始地址），这样使用起来更加方便。

2.文件操作——打开和关闭

fopen()

FILE *fopen(const char *filename, const char *mode)

fopen("C:\\", w); //绝对路径
fopen("".\\source\\mode.png")"， w)// 这里的.\表示的是当前目录（一般是和.c文件所在的）
fopen(""./source/mode.png")"， w)// 使用/就是不用搞转义了。

文件使用方式	含义	如果指定文件不存在
“r”(只读)	为了输入数据，打开一个已经存在的文本文件	出错
“w”(只写)	为了输出数据，打开一个文本文件	建立一个新的文件
“a”(追加)	向文本文件尾添加数据	建立一个新的文件
“rb”(只读)	为了输入数据，打开一个二进制文件	出错
“wb”(只写)	为了输出数据，打开一个二进制文件	建立一个新的文件
“ab”(追加)	向一个二进制文件尾添加数据	出错
“r+”(读写)	为了读和写，打开一个文本文件	出错
“w+”(读写)	为了读和写，建一个新的文件	建立一个新的文件
“a+”(读写)	打开一个文件，在文件尾进行读写	建立一个新的文件
“rb+”(读写)	为了读和写打开一个二进制文件	出错
“wb+”(读写)	为了读和写，新建一个新的二进制文件	建立一个新的文件
“ab+”(读写)	打开一个二进制文件，在文件尾进行读和写	建立一个新的文件

注：当使用“w”，“wb”，“w+”，“wb+”打开文件时会清除文件原本存储的数据。

fclose()

该函数的返回值是int类型的：如果关闭成功就返回0值，否则返回EOF（-1）值。

int main()
{
	//打开
	FILE* pf = fopen("text.txt","w");
	//判断是否打开成功
	if (pf == NULL)
	{
		perror("fopen");
		return 1;
	}
	//关闭
	if (fclose(pf) == EOF)
	{
		//关闭失败
		perror("fclose");
		return 1;
	}
	pf = NULL;
	return 0;
}

rename()

int rename(const char *old_filename, const char *new_filename)

如果成功，则返回零。如果错误，则返回 -1，并设置 errno。

int ret;
char oldname[] = "file.txt";
char newname[] = "newfile.txt";

ret = rename(oldname, newname);

if(ret == 0) 
{
   printf("文件重命名成功");
}
else 
{
   printf("错误：不能重命名该文件");
}

fflush

int fflush(FILE *stream)

• 如果成功刷新缓冲区，fflush() 返回 0。

• 如果发生错误，返回 EOF，并且设置错误标识符（ferror）。

• 如果 stream 为 NULL，则会刷新所有输出流的缓冲区。

• 如果 stream 是文件指针，则刷新该文件流的输出缓冲区。

3.顺序读写

fputc

当该函数成功运行时返回所存入字符的ASCII码值，否则返回EOF（-1）值。

FILE* pf = fopen("text.txt", "w");
//写入数据
int i = 'a';
for (i = 0; i < 26; i++)
{
       fputc('a' + i, pf);
}
//这时候，pf就是字母表：abcde...了

fgetc

该函数成功读入数据时会返回读取字符的ASCII值，反之则会返回EOF（-1）值。

FILE* pf = fopen("text.txt", "r");//此时读取文件要用"r"的方式打开
while ((i = fgetc(pf)) != EOF)
{
	printf("%c ", i);
}

fputs

fputs("hello", pf);
fputs("world", pf);

fgets

该函数只能读取一行的数据

char *fgets(char *str, int n, FILE *stream)

如果成功，该函数返回相同的 str 参数。如果到达文件末尾或者没有读取到任何字符，str 的内容保持不变，并返回一个空指针。

如果发生错误，返回一个空指针。

可以使用连续的fgets读取到两行。

FILE* fp;
char str[20];
fp = fopen("file.txt", "w+");
fputs("abc\ndefgn", fp);
fclose(fp);

fp = fopen("file.txt", "r");
fgets(str, 8, fp);
while (fgets(str, 20, fp) == NULL)
	continue;
fputs(str, stdout);
fclose(fp);
fp = NULL;

fprintf

int fprintf(FILE *stream, const char *format, ...)

如果成功，则返回写入的字符总数，否则返回一个负数。

类似sprintf，不过一个写入对象是文件，一个是字符串

fprintf(fp, "%s %s %s %d", "We", "are", "in", 2014);   

fscanf

int fscanf(FILE *stream, const char *format, ...)

如果成功，该函数返回成功匹配和赋值的个数。如果到达文件末尾或发生读错误，则返回 EOF。

注意，一般而言，fscanf遇到空格便会停止对这个的读取。

   char str1[10], str2[10], str3[10];
   int year;
   FILE * fp;

   fp = fopen ("file.txt", "w+");
   fputs("We are in 2014", fp);
   
   rewind(fp);
   fscanf(fp, "%s %s %s %d", str1, str2, str3, &year);
   
   printf("Read String1 |%s|\n", str1 ); // We
   printf("Read String2 |%s|\n", str2 ); // are
   printf("Read String3 |%s|\n", str3 );
   printf("Read Integer |%d|\n", year );

   fclose(fp);
   
   return(0);
}

fwrite

size_t fwrite(const void *ptr, size_t size, size_t nmemb, FILE *stream)

• ptr – 这是指向要被写入的元素数组的指针。
• size – 这是要被写入的每个元素的大小，以字节为单位。
• nmemb – 这是元素的个数，每个元素的大小为 size 字节。
• stream – 这是指向 FILE 对象的指针，该 FILE 对象指定了一个输出流。

struct S L = { 20,"李四","女" };
FILE* pf = fopen("text.txt", "wb");//二进制输出时用wb

fwrite(&L, sizeof(struct S), 1, pf);

就是把L里面的数据，写入到文件中。

fread

size_t fread(void *ptr, size_t size, size_t nmemb, FILE *stream)

• ptr – 这是指向带有最小尺寸 size*nmemb 字节的内存块的指针。
• size – 这是要读取的每个元素的大小，以字节为单位。
• nmemb – 这是元素的个数，每个元素的大小为 size 字节。
• stream – 这是指向 FILE 对象的指针，该 FILE 对象指定了一个输入流。

struct S s;
FILE* pf = fopen("text.txt", "rb");//二进制输出时用rb
if (fread(&s, sizeof(struct S), 1, pf) != 0)// 其返回读取的次数
{
	printf("%d %s %s", s.age, s.name, s.sex);
}

sprintf与sscanf

	对于sprintf函数它可以将各种数据以各种格式（如%d，%s，%c等等）转换为字符串类型输入到char*类型的str参数中。

​ 对于sscanf函数它可以将字符串类型的str参数的数据以各种格式（如%d，%s，%c等等）输出到各变量中。

struct S
{
	int age;
	char name[20];
	float point;
};
int main()
{
	struct S l = { 15,"lisi",88.9f };
	char arr[20];
	struct S j = { 0 };
	//将各类型数据转换为字符串
	sprintf(arr, "%d %s %.1f", l.age, l.name, l.point);
	printf("%s\n", arr);
	//将字符串数据转换为各种类型
	sscanf(arr, "%d %s %f", &(j.age), j.name, &(j.point));
	printf("%d %s %.1f", j.age, j.name, j.point);
	return 0;
}

4.随机读写

fseek

int fseek(FILE *stream, long int offset, int whence)

该函数运行成功，返回零。否则回非零值。

• stream – 这是指向 FILE 对象的指针，该 FILE 对象标识了流。

• offset – 这是相对 whence 的偏移量，以字节为单位。

• whence – 这是表示开始添加偏移 offset 的位置。它一般指定为下列常量之一：

• 常量	描述
  SEEK_SET	文件的开头
  SEEK_CUR	文件指针的当前位置
  SEEK_END	文件的末尾

FILE* pf = fopen("text.txt", "r");
//设置pf指针从文件起始位置向后偏移3个单位
fseek(pf, 3, SEEK_SET);
//读入数据
int i = fgetc(pf);
printf("%c", i);

ftell

long int ftell(FILE *stream)

成功后，返回位置指示器的当前值。失败时，返回 -1L，并将 errno 设置为系统特定的正值。

//设置偏移量
fseek(pf, 0, SEEK_END);
//计算偏移量
printf("%d", ftell(pf));

rewind

该函数可以将所传入的文件指针设置指向文件初始位置。

文件缓冲区

int main()
{
	//打开
	FILE* pf = fopen("text.txt", "wb");
	if (pf == NULL)
	{
		perror("fopen");
		return 1;
	}
	//存入
	int a = 10000;
	fwrite(&a, sizeof(int), 1, pf);
	printf("此20秒数据在文件缓冲区内，打开文件是没有数据的\n");
	Sleep(20000);//睡眠10秒
	fflush(pf);//此函数可以刷新缓冲区中的数据，使其存入硬盘文件中
	printf("此20秒数据从文件缓冲区内读入到文件中，打开文件是有数据的\n");
	Sleep(20000);
	//关闭
	fclose(pf);
	pf = NULL;
	return 0;
}

因为有缓冲区的存在，C语言在操作文件的时候，需要做刷新缓冲区或者在文件操作结束的时候关闭文件。
如果不做，可能导致读写文件的问题。

这也就是说，如果我们不用fflush，如果我们在一个fopen里面写入、然后读取是会失败的。

顺序线性表

定义

typedef struct {
    ElemType* elem;
    int length;     //当前长度
    int listsize;   //当前分配量
}Sqlist;

初始化

 void init_list(Sqlist &L){  // C++语法。可以认为，把形参（值传递）变成实参。相当于Sqlist *L。
	L.elem = (ElemType *) malloc(LIST_INIT_SIZE * sizeof(ElemType));
	if (!L.elem) exit(OVERFLOW);
	L.length = 0;
	L. listsize = LIST_INIT_SIZE;
}

置零

Status ClearList_Sq(SqList& L)
{
    L.length = 0;
    return OK;
}

销毁

Status DestroyList_Sq(SqList& L) {
    free(L.elem);
    L.elem = NULL;
    L.length=0;
    L.listsize=0;
    return OK;
}

是否空表

Status ListEmpty(SqList L)
{
    if (L.length == 0) return TRUE;
    else return FALSE;
}

返回第i个元素

Status GetElem_Sq(SqList L, int i, ElemType& e)
{
    if (i<1 || i>L.length) {
        printf("超过表长");
        exit(EXIT_FAILURE);
    }
    else 
    e = L.elem[i - 1];
    return OK;
}

定位一个元素，返回次序

Status LocateElem_Sq(SqList L, ElemType choose, int (*func)(ElemType, ElemType))
{
    if (L.length == 0) return ERROR;
    int i;
    for (i = 0; i < L.length; i++) {
        if (func(choose, L.elem[i]) == 1)
        {
            return i + 1;
        }
    }
    return 0;
}

插入

Status ListInsert_Sq(SqList& L, int i, ElemType e) {
    if (i<1 || i>L.length) return ERROR;
    if (L.length > L.listsize)
    {
        ElemType* newbase = (ElemType*)realloc(L.elem, (L.listsize + LISTINCREASE) * sizeof(ElemType));
        if (!newbase) exit(OVERFLOW);
       // free(L.elem);
        L.elem = newbase;
        L.listsize += LISTINCREASE;
    }
    ElemType* q = &(L.elem[i - 1]);
    for (ElemType* p = &(L.elem[L.length - 1]); p >= q; --p)
    {
        *(p + 1) = *p;
    }
    *q = e;
    ++L.length;
    return OK;
}

删除

Status ListDelet_Sq(SqList& L, int i, ElemType& e) 
{
    if (i<1 || i>L.length) return ERROR;

    ElemType* p = &(L.elem[i - 1]);
    e = *p;
    ElemType* q = L.elem + L.length - 1; //指向最后一位。L.elem为首地址，后面为移动位数
    //为什么不写成 = &(L.elem[L.length - 1])  ??
    for (++p; p <= q; ++p)
    {
        *(p - 1) = *p;
    }
    --L.length;
    return OK;
}

线性表赋值★

void Sq_input(SqList& L) {
    printf("请依次输入顺序线性表的数字，用空格分隔\n");
    char* str = (char*)malloc(L.listsize);
    if (!str) {
        printf("内存分配失败\n");
        return;
    }

    if (!fgets(str, L.listsize, stdin)) {
        printf("读取输入失败\n");
        free(str);
        return;
    }

    char* token = NULL;
    char* endptr = NULL;
    const char* delimiters = " \t\n";  // 扩展分隔符
    int i = 0;

    token = strtok(str, delimiters);
    while (token != NULL && i < L.listsize) {
        long num = strtol(token, &endptr, 10);

        // 验证转换有效性
        if (*endptr != '\0' || endptr == token) { 
        //分析：若强制传入空字符串（如 token = ""），此时：strtol 返回 0，endptr == token（即指向空字符串起始位置）。
		//*endptr == '\0'，条件 *endptr != '\0' 不成立，会错误接受该 token 为数字 0。
		
            printf("跳过非法输入: %s\n", token);
            token = strtok(NULL, delimiters);
            continue;
        }

        L.elem[i++] = (int)num;
        L.length++;
        token = strtok(NULL, delimiters);
    }

    printf("成功输入 %d 个有效数字\n", i);
    free(str);
}

线性链表

单链表

参考链接：【数据结构】链表(单链表实现+详解+原码)-CSDN博客 | 数据结构——图解单链表的初始化、赋值和遍历输出C语言_将链表原始赋值-CSDN博客 |

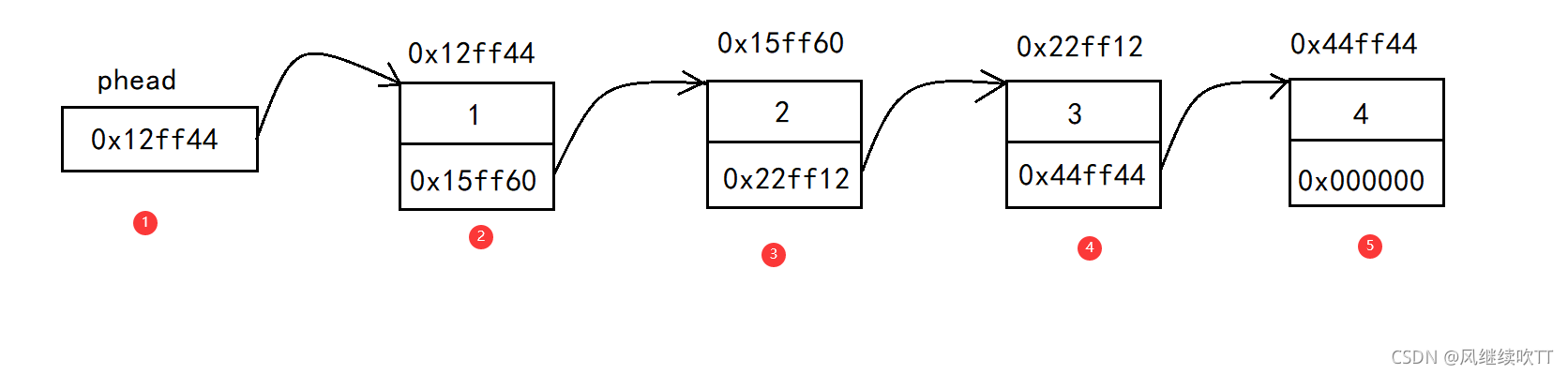
定义

typedef struct LNode {
    ElemType data;
    struct LNode* next;
}LNode, *LinkList; 
// 这里的Lnode并不会有问题，我们也习惯这么做
// 即LNode名称相同。

也就是说，一个LNode（节点），包含两个数据：data和一个指针（指向结构体）。这里定义的LinkList是一个头指针，指向头节点（下图中的phead，当然也可以不用）。

这里我们需要注意，所有的结点在代码中均表现为结构指针，所以我们用 -> 来进行读取和赋值

打印（示例）

//打印链表
void SListPrint(SListNode* phead)
{
	SListNode* cur = phead;//一般不直接移动头指针，而是创建一个指针变量来移动
	while (cur)//当指针为空时结束循环
	{
		printf("%d->", cur->data);//打印该结点的数据
		cur = cur->next;//将指针指向下一个结点
	}
	printf("NULL\n");
}

赋值★

已知数组，插入链表。

//申请结点
LNode * CreateList(ElemType x) {
	LinkList newnode = (LinkList)malloc(sizeof(LNode));
	if (!newnode) {
		perror("malloc");
		exit(-1);
	}
	newnode->data = x;
	newnode->next = NULL;
	return newnode;
}

头插入

void List_Push_Front(LinkList& phead, ElemType x) {
    LinkList newnode = CreateList(x);
    newnode->next = phead->next;
    phead ->next = newnode;
}

尾插入

void List_Pust_Back(LinkList& phead, ElemType x) {
    LinkList newnode = CreateList(x);
    if (!phead->next) {
        phead->next = newnode;
    }
    else {
        LinkList end = phead;
        while (end->next) {
            end = end->next;
        }
        end->next = newnode;
    }
}// 当然，我们其实可以传入end指针（指向尾结点）

销毁

void Delete_List(LinkList& phead) {
    while (phead) {
        LinkList next = phead->next;
        free(phead);
        phead = next;
    }
}

删除元素——定位链表元素

Status Delete_elem(LinkList& L, int i) {
    LinkList p = L;
    int j = 0;
    while (j < i - 1 && p ->next) {
        j++;
        p = p->next;
    }
    if (!(p->next) || j > i - 1) exit(-1);
    LinkList q = p->next;
    p->next = q->next;
    free(q);
    q = NULL;
    return OK;
}

翻转

void reverse_Link(LinkList& phead) {
	if (!phead) exit(ERROR);
	
	LinkList prev = NULL;
	LinkList next = NULL;
	LinkList current = phead;
	current = current->next;

	while (current) {
		next = current->next;  // 保存下一个节点
		current->next = prev;  // 反转当前节点的指针
		prev = current;        // 移动prev到当前节点
		current = next;        // 移动current到下一个节点
	}
	phead->next = prev;
}

静态链表

定义

typedef struct{
	ElemType data;
	int cur; //表明其在数组中的位置
}component, SLinkList[MaxSize];

双向链表

定义

typedef struct DuLNode{
	ElemType data;
	struct DuLNode *prior;
	struct DuLNode *next;
} DuLNode, *DuLinkList;

插入

Status ListInsert(DuLinkList &L, int i, ElemType e){
略。
}

应用1：一元多项式运算

待完善和补充

栈

顺序栈

定义

栈先进后出

typedef struct {
	int y; // 行
	int x; // 列
}ElemType; // 例子，可以改

typedef struct {
	ElemType* top;
	ElemType* base;
	int stacksize;
}SqStack;

初始化

void init_stack(SqStack& T) {
	T.top = (ElemType*)malloc(MAXSIZE*sizeof(ElemType)); 
	T.base = T.top;
	T.stacksize = MAXSIZE;
}

获取头元素

int Get_top_elem(SqStack T, ElemType &e) {
	if (T.base == T.top) return ERROR;
	e = *(T.top - 1);
	return OK;
}

入栈

void push_stack(SqStack& T,int map[][Map_col], ElemType e) {
	if (T.top - T.base >= T.stacksize) {
		T.base = (ElemType*)realloc(T.base, 
			(T.stacksize + SIZEADD) * sizeof(ElemType));
		if (!T.base) {
			perror("malloc");
			exit(-1);
		}
			T.top = T.base + T.stacksize;
			T.stacksize += SIZEADD;
	}
	*T.top++ = e;
}

出栈

void pop_stack(SqStack& T,int map[][Map_col], ElemType &e) {
	if (T.base == T.top) exit(-1);
	e = * --T.top;
}

清空栈

void clear_stack(SqStack& T) {
	if (T.base != NULL) {
		T.top = T.base;
	}
}

销毁栈

void destroy_stack(SqStack& T) {
	if (T.base != NULL) { // 检查栈是否已初始化
		free(T.base); // 释放栈底内存
		T.base = NULL;
		T.top = NULL;
		T.stacksize = 0;
	}
}

链栈

简单来说，就是单链表，不过，其插入的方式为头插入，即若我输入123456，那么，链表储存的是654321。这样就实现了先进后出。然后每入栈便malloc，出栈便free。

以下 为参考代码

定义

typedef struct StackNode {
    char data;
    struct StackNode* next;
} StackNode;

typedef struct {
    StackNode* top;
    int size;
} LinkedStack;

入栈

注意，这里的top就是指向了第1个元素，并未安排头结点

void push(LinkedStack* stack, char value) {
    StackNode* newNode = (StackNode*)malloc(sizeof(StackNode));
    if (!newNode) {
        printf("内存分配失败\n");
        exit(EXIT_FAILURE);
    }
    newNode->data = value;
    newNode->next = stack->top;
    stack->top = newNode;
    stack->size++;
}

出栈

char pop(LinkedStack* stack) {
    if (isEmpty(stack)) {
        printf("栈下溢错误\n");
        exit(EXIT_FAILURE);
    }
    StackNode* temp = stack->top;
    char popped = temp->data;
    stack->top = stack->top->next;
    free(temp);
    stack->size--;
    return popped;
}

队列

定义

typedef struct QueueNode {
    BiTNode* treeNode;
    struct QueueNode* next;
} QueueNode;

// 队列结构
typedef struct Queue {
    QueueNode* front; // 队首
    QueueNode* rear;  // 队尾
} Queue;

初始化

// 初始化队列
void initQueue(Queue* q) {
    q->front = q->rear = NULL;
}

入队

void enqueue(Queue* q, BiTNode* node) {
    QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));
    if (!newNode) {
        printf("Memory allocation failed\n");
        exit(1);
    }
    newNode->treeNode = node;
    newNode->next = NULL;

    if (isQueueEmpty(q)) {
        q->front = q->rear = newNode;
    }
    else {
        q->rear->next = newNode;
        q->rear = newNode;
    }
}

出队

BiTNode* dequeue(Queue* q) {
    if (isQueueEmpty(q)) {
        printf("Queue is empty\n");
        exit(1);
    }

    QueueNode* temp = q->front;
    BiTNode* treeNode = temp->treeNode;

    q->front = q->front->next;
    if (q->front == NULL) {
        q->rear = NULL; // 如果队列为空，重置队尾指针
    }

    free(temp); // 释放队列节点
    return treeNode;
}

串

待补充

数组

待补充

二叉树

普通二叉树

定义

typedef int TElemType;

typedef struct BiTNode {
    TElemType data;
    struct BiTNode* lchild, * rchild;
}BiTNode, *BiTree;

完全二叉树建立——队列

BiTNode* createNode(TElemType data) {
    BiTNode* newNode = (BiTNode*)malloc(sizeof(BiTNode));
    if (!newNode) {
        printf("Memory allocation failed\n");
        exit(1);
    }
    newNode->data = data;
    newNode->lchild = NULL;
    newNode->rchild = NULL;
    return newNode;
}

BiTree buildCompleteBinaryTree(int arr[], int n) {
    if (n == 0) return NULL;

    // 创建根节点
    BiTree root = createNode(arr[0]);

    // 初始化队列
    Queue q;
    initQueue(&q);

    // 根节点入队
    enqueue(&q, root);

    int i = 1;

    while (i < n) {
        BiTNode* current = dequeue(&q);

        // 添加左子节点
        if (i < n) {
            current->lchild = createNode(arr[i++]);
            enqueue(&q, current->lchild);
        }

        // 添加右子节点
        if (i < n) {
            current->rchild = createNode(arr[i++]);
            enqueue(&q, current->rchild);
        }
    }

    return root;
}

二叉树遍历——递归实现

先序遍历

//先序遍历
void PrevOrder(BTNode* root)
{
	if (root == NULL)//递归终止条件，若遍历到空，则返回
	{
		printf("NULL");
		return;
	}
	printf("%d", root->data);//先序遍历，先输出根节点的值
	PrevOrder(root->left);//递归进入左子树
	PrevOrder(root->right);//递归进入右子树
}

中序遍历

//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL");
		return;
	}
	InOrder(root->left);
	printf("%d", root->data);  // 这里可以换成别的函数，用于遍历操作
	InOrder(root->right);
}

后序遍历

//后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d", root->data);
}

层次遍历——队列实现

void LevelOrder(BTNode* root)//层序遍历按行输出
{
	Queen q;//创建队列
	QueenInit(&q);//队列初始化
	int levelsize = 0;//用来统计每层的节点个数
	if (root)//根节点不为空
	{
		QueenPush(&q, root);//进入队列
		levelsize = 1;//第一层的节点个数为1
	}
	while (!QueenEmpty(&q))//循环条件：队列是否为空
	{
		while (levelsize--)//层节点
		{
			BTNode* front = QueenFront(&q);//取出队头数据
			printf("%d ", front->data);//输出队头数据
			QueenPop(&q);//因为已经取出数据，删除队头数据，队头数据更新
			if (front->left)//左孩子不为空，进入队列
			{
				QueenPush(&q, front->left);
			}
			if (front->right)//右孩子不为空，进入队列
			{
				QueenPush(&q, front->right);
			}
		}
		printf("\n");//换行输出
		levelsize = QueenSize(&q);//计算队列中的节点数量
	}
	QueenDestroy(&q);//销毁队列
}

非递归遍历——栈

先序

//先序遍历二叉树
void PreOrder(BiTree T)
{
	SqStack* S;
	S = InitStack();
	BiTreeNode* p;
	p = T; //  头结点，指向二叉树的根结点
	while (p|| !StackEmpty(*S))
	{
		if (p) // 非空
		{
			printf("%c",p->data);
			Push(S, p); // 入栈 p
			p = p->LChild;
		}
		else  // 为空时， 弹出上一个指向的指针
		{
			Pop(S, p); // p接收返回值， 注意，这里栈的值，代表的是指向的节点
			p = p->RChild;
		}
	}
}

中序

//中序遍历二叉树
void InOrder(BiTree T)
{
	SqStack* S;
	S = InitStack();
	BiTreeNode* p;
	p = T;
	while (p || !StackEmpty(*S))
	{
		if (p)
		{
			Push(S, p);
			p = p->LChild;
		}
		else
		{
			Pop(S, p);
			printf("%c", p->data);
			p = p->RChild;
		}
	}
}

后序

void PostOrder(BiTree &T) {  // 全篇
    SqStack s;
    InitStack(s);
    BiTree  p = T,  r = NULL; // r标记最近访问过的结点
    while (p != NULL || !StackEmpty(s)) {
        if (p != NULL) {
            push_stack(s, p);  // 一直向左走，左孩子入栈
            p = p->lchild;
        }
        else {
          //  GetTop(s, p);
            p = *(s.top - 1);
            // 获取s的栈顶元素赋值给p
            // GetTop(s,p)意思就是判断栈顶元素的情况
            //
            if (p->rchild && p->rchild != r) {
                // 若右孩子存在且未被访问
                p = p->rchild;  // 就让右孩子
                push_stack(s, p);  // 入栈
                p = p->lchild;  // 让右孩子向左
                //上面三句意思就是让右孩子的左孩子一直入栈，一直向左走
            }
            // 
            else {
                pop_stack(s, p);  // 右孩子为空或未被访问过，就出栈
                printf(" %d ",p->data);
                r = p;  // r标记最近访问结点
                p = NULL;  // r置空
                // 置空原因：因为这个结点已经出栈了
                //继续指向就没必要了，置空后r不标记任何结点
            }
        }
    }
}

赋值

//通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(char* a, int n, int* pi)
{
	if (*pi >= n)//如果索引>=数组的长度，直接返回
		return;
	if (a[*pi] == '#')//如果当前数组的数据是‘#’，则说明此时的节点是NULL，直接返回
	{
		(*pi)++;//索引往后迭代
		return NULL;
	}
	//因为通过前序遍历数组创建二叉树，所以先创建父节点，再创建它的左、右孩子节点
	BTNode* root = BuyBTNode(a[(*pi)++]);//根据当前索引的字符创建父节点，索引迭代
	root->left = BinaryTreeCreate(a, n, pi);//递归创建左孩子节点
	root->right = BinaryTreeCreate(a, n, pi);//递归创建右孩子节点
	return root;//返回创建的父节点
}

销毁

void BinaryTreeDestory(BTNode* root)
{
	if (root == NULL)
		return;
	//后序遍历删除节点
	BinaryTreeDestory(root->left);
	BinaryTreeDestory(root->right);
	free(root);
}

计算二叉树结点

int countNodes(BiTree root) {
    if (root == NULL) {
        return 0; // 空节点返回 0
    }
    return 1 + countNodes(root->lchild) + countNodes(root->rchild);
}

线索二叉树

• 若结点的左子树为空，则该结点的左孩子指针指向其前驱结点
• 若结点的右子树为空，则该结点的右孩子指针指向其后继结点

这种指向前驱和后继的指针称为线索，将一棵普通的二叉树以某种次序遍历，并添加线索的过程称为线索化。

定义

typedef enum PointerTag { Link, Thread}; // Link == 0 :指针， Thread == 1:线索
typedef struct BiThrNode{
	TElemType data;
	struct BiThrNode *lchild, *rchild;
	PointerTag  LTag, RTag;
}BiThrNode, *BiThrTree;

遍历算法

Status InOrderTraverse_Thr(BiThrTree T, Status(*Visit)(TElemType e)) {

	p = T->lchild;
	while (p != T) {
		whlie(p->LTag == Link) p = p->lchild;
		Visit(p->data);
		whlile(p->RTag == Thread && p->rchild != T) {
			p = p->rchild;
			Visit(p->data);
		}
		p = p->rchild;
	}
	return OK;
}

二叉排序树

略，待补充。。。

二叉树的直观打印

参考链接：控制台图形化打印二叉树(c/c++)_c++打印二叉树-CSDN博客 |

bug: 这里改成了二叉树是int类型的，bug是无法正确打印printBiTree中的判断数：有3个，分别代表空格/ \

int width, height;

void fillArray(BiTree& T, int* a, int i, int j)
{
    int ti = -1;
    int tj = -1;
    if (T) //如果该位置有节点
    {
        *(a + (i * width) + j) = T->data; //向数组该点填入字符
        if (T->lchild) //有左右孩子给对应的连接线,左右孩子的值在下一层递归赋
        {
            //将该点与其左孩子之间的连线全部填上'/'
            for (ti = i + 1, tj = j - 1; tj > j - (height - i + 1) / 2; tj--)
            {
                *(a + ((ti)*width) + tj) = -99;
                ti++;
            }
        }
        if (T->rchild)
        {
            for (ti = i + 1, tj = j + 1; tj < j + (height - i + 1) / 2; tj++)
            {
                *(a + ((ti)*width) + tj) = 99;
                ti++;
            }
        }
        //经过循环,ti恰好指到其孩子所在的层
        fillArray(T->lchild, a, ti, j - (height - i + 1) / 2);
        fillArray(T->rchild, a, ti, j + (height - i + 1) / 2);
    }
}
int DeepTree(BiTree T)
{
    if (!T)
    {
        return 0;
    }
    return DeepTree(T->lchild) > DeepTree(T->rchild) ? DeepTree(T->lchild) + 1 : DeepTree(T->rchild) + 1;
    //关键代码:如果该节点的左子树深度大于右子树则将左子树的深度加一返回,这个返回值便是以该节点做根节点的树的深度,右子树深度大时则相反
}
void printBiTree(BiTree& T)
{
    int i, j;
    int n = DeepTree(T); //计算出深度n
    //在计算机中数据以二进制形式存储,所以一个数据左移1位就相当于乘以2的1次方
    width = (2 << n) - 3;  // 2^(n+1)-3
    height = (2 << (n - 1)) - 1; // 2^n-1
    int* a = (int*)malloc(sizeof(int) * (width * height)); // 申请空间
 //   if (!a) exit(-1);
  //  memset(a, 88, sizeof(a));
    if (!a) {
        perror("malloc");
        exit(-1);
    }
    // 空间初始化为0
    for (i = 0; i < height; i++)
    {
        for (j = 0; j < width; j++)
        {
            *(a + (i * width) + j) = -88;
        }
    }

    //调用之前定义好的函数,填充打印数组
    fillArray(T, a, 0, (width - 1) / 2);

    //根据打印数组的内容来实现打印
    for (i = 0; i < height; i++)
    {
        for (j = 0; j < width; j++)
        {
            if (*(a + (i * width) + j) == -99)
            {
                printf("/");
            }
            else if (*(a + (i * width) + j) == 99)
            {
                printf("\\");
            }
            else if (*(a + (i * width) + j) == -88 )
            {
                printf(" ");
            }
            else
            {
                printf("%d", *(a + (i * width) + j));
            }
        }
        printf("\n");
    }
}

哈夫曼树

定义

最优二叉树，带路径的权值总和最小。哈夫曼树中权越大的叶子离根越近。

构造

每次选权值最小的两个结点，构造成一个新树，新数的权值为二者之和。以此类推。

——包含n个叶子结点的哈夫曼树中共有2n-1个结点

——只有度为0或２的结点，没有度为１的结点

算法实现如下：采用顺序存储的结构

typedef struct {
    unsigned int weight;
    unsigned int parent, lchild, rchild;
} HTNode, * HuffmanTree;

// 创建哈夫曼树
void CreateHuffmanTree(HuffmanTree* HT, int n, int* weights) {
    if (n <= 1) return;
    int m = 2 * n - 1;
    *HT = (HuffmanTree)malloc((m + 1) * sizeof(HTNode));
    HuffmanTree p = *HT;

    // 初始化
    for (int i = 1; i <= m; ++i) {
        p[i].weight = (i <= n) ? weights[i - 1] : 0;  // 编号为1 - n的 权值为概率。其他均为0
        p[i].parent = p[i].lchild = p[i].rchild = 0;  // 初始化为0
    }

    // 构建哈夫曼树
    for (int i = n + 1; i <= m; ++i) {    //需要执行 2n-1-n = n-1次。因为共n个初值。
        int s1, s2;
        Select(*HT, i - 1, &s1, &s2);
        (*HT)[s1].parent = (*HT)[s2].parent = i;   // 父母结点指向
        (*HT)[i].lchild = s1;                      // 左右孩子
        (*HT)[i].rchild = s2;
        (*HT)[i].weight = (*HT)[s1].weight + (*HT)[s2].weight;  //权值为和
    }
}

// 选择两个最小权重的节点
void Select(HuffmanTree HT, int n, int* s1, int* s2) {  // s1，s2为最小值在线性表中的序号
    int min1 = 0x7fffffff, min2 = 0x7fffffff;
    *s1 = *s2 = 0;

    for (int i = 1; i <= n; ++i) {
        if (HT[i].parent == 0 && HT[i].weight < min1) {
            min2 = min1;
            *s2 = *s1;
            min1 = HT[i].weight;
            *s1 = i;
        }
        else if (HT[i].parent == 0 && HT[i].weight < min2) {
            min2 = HT[i].weight;
            *s2 = i;
        }
    }
}

void  fun_task_6() {
    int weights[] = { 7, 19, 2, 6, 32, 3, 21, 10 };
    int n = sizeof(weights) / sizeof(weights[0]);
    char chars[] = { 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h' };

    HuffmanTree HT;
    HuffmanCode HC;

    CreateHuffmanTree(&HT, n, weights);
    HuffmanCoding(HT, &HC, n);
    PrintHuffmanCode(HC, chars, n);

}

哈夫曼编码

代码如下，其他代码为上面的哈夫曼树的构造

typedef char** HuffmanCode;

// 生成哈夫曼编码
void HuffmanCoding(HuffmanTree HT, HuffmanCode* HC, int n) {
    char* cd = (char*)malloc(n * sizeof(char));
    cd[n - 1] = '\0';

    *HC = (HuffmanCode)malloc((n + 1) * sizeof(char*));
    for (int i = 1; i <= n; ++i) {
        int start = n - 1; // 最大编码数量
        for (int c = i, f = HT[i].parent; f != 0; c = f, f = HT[f].parent) {
            if (HT[f].lchild == c) cd[--start] = '0'; //字符为左孩子，则赋0，倒退循环
            else cd[--start] = '1';
        }
        (*HC)[i] = (char*)malloc((n - start) * sizeof(char));
        strcpy((*HC)[i], &cd[start]); //第i个字符的哈夫曼编码，从start，这样对应前面的start--，方便了赋值
    }
    free(cd);
}

// 打印哈夫曼编码
void PrintHuffmanCode(HuffmanCode HC, char* chars, int n) {
    printf("Huffman Codes:\n");
    for (int i = 1; i <= n; ++i) {
        printf("%c: %s\n", chars[i - 1], HC[i]);
    }
}

图（难）

基本

很多，略

构造

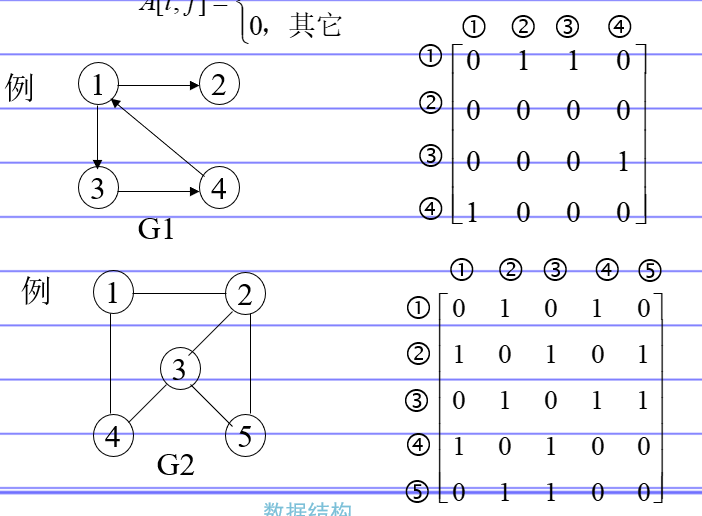
1. 邻接矩阵表示

   

typedef enum {DG,DN,UDG,UDN} GraphKind; // 四种类型：有向图，有向网...
typedef struct ArcCell {
	int adj;  // 在图中，为0表示不相接，为1是相接。 在网中（带权值） 无穷大数（或者0）表示不相接，权值代表相接
	infoType *info; //该弧的相关信息
}ArcCell, AdjMatrix[10][10]; // 后面那个便是上面的邻接矩阵10*10的

typedef struct{
	AdjMatrix arcs; //邻接矩阵
	int vexnum, arcnum; 顶点数和弧数。
	GraphKind kind; // 图的种类标志
}

for(i=0; i<G.arcnum; i++){
	scanf(v1,v2,w); //输入一条边的顶点和权值
	i = LocateVex(T,v1);
	j = LocateVex(T,v2);
	T.arcs[i][j].adj = w; 
	...
}

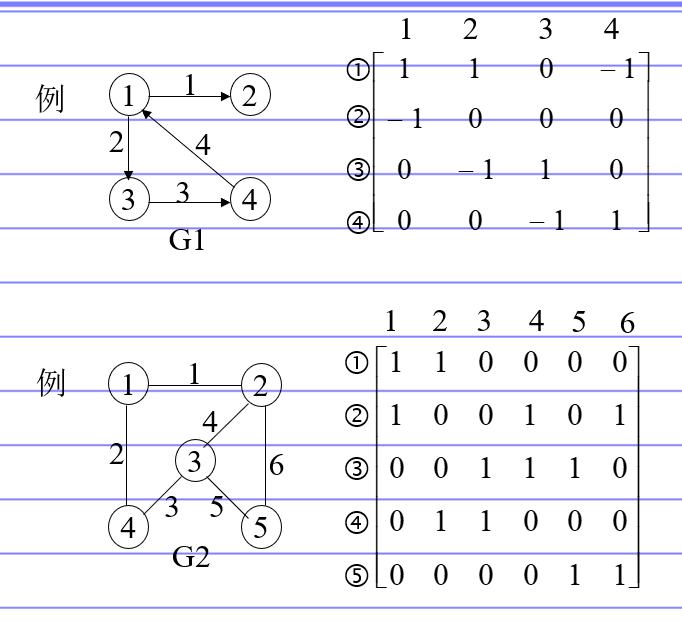
2. 关联矩阵表示

x轴表示的是弧，y轴表示的是边。有向图中，-1表示入度。

算法：待日后补充

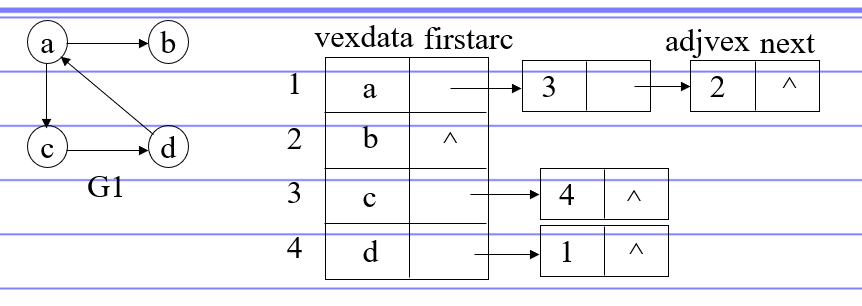
3. 邻接表 表示（重点）

简单来说就是利用一组链表来表示

有向图的逆邻接表：有向图中对每个结点建立以Vi为头的弧的单链表。就是按照入度来搞

typedef struct ArcNdoe {
	int adjvex; //该弧指向的顶点的位置
	struct ArcNode *nextarc;
}ArcNode;
typedef struct VNode {
	VertexType data; //顶点的信息，比如上面的 a b c
	ArcNode *firstarc;  // 一个头指针
}VNode, AdjList[10];// 10 为定义的最大结点数
typedef struct {
	AdjList vertices;
	int vexnum, arcnum;
	int kind;
}ALGraph;

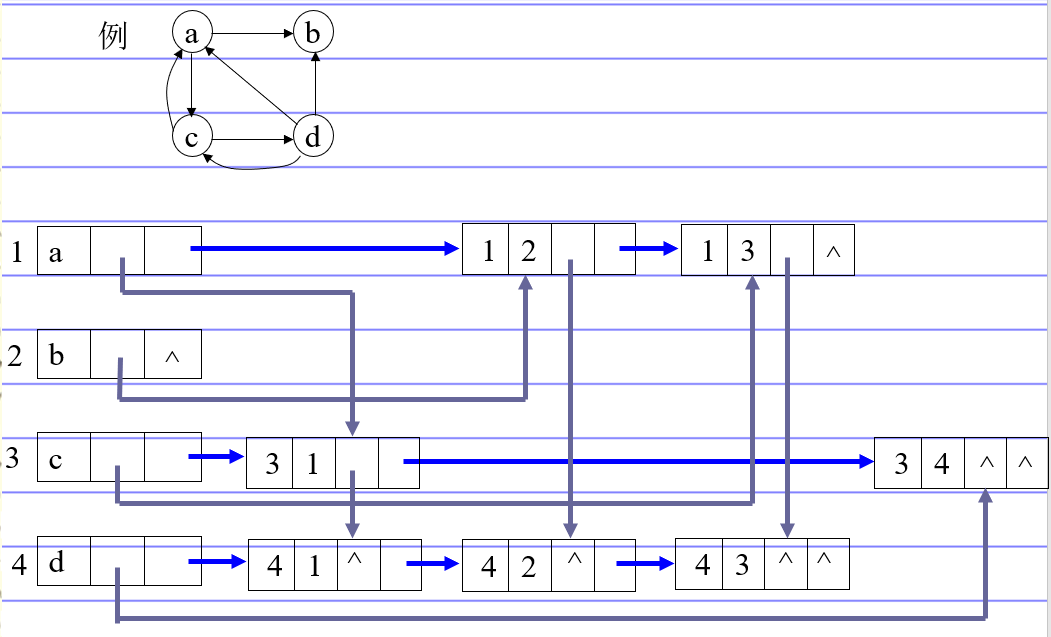
4. 有向图的十字链表 表示法

水平指针为出度，垂直指针为入度。

typedef struct ArcBox {
	int tailvex, headvex;		// 该弧的头尾
	struct ArcBox *hlink, *tlink; //指向与弧头相同和弧尾相同的链
}ArcBox;
typedef struct VexNode {
	VertexType data; 
	ArcBox *firstin, *firstout; //头结点的两个指针
}VexNode;
typedef struct {
	VexNode xlist[10];
	int vexnum,arcnum;
}

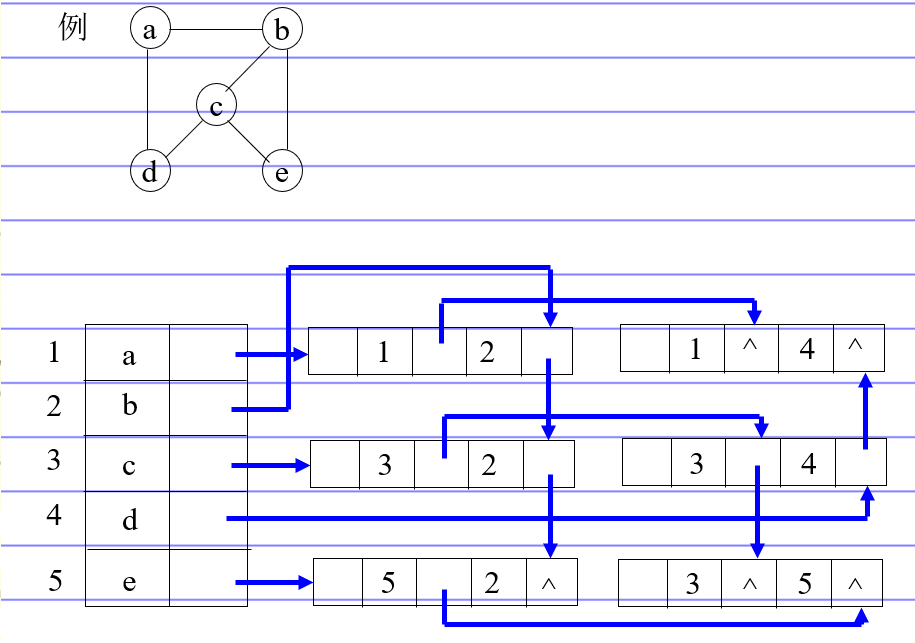
5. 无向图的邻接多重表

typedef enum {unvisited, visited} VisitIf;
typedef struct EBox {
	VisitIf mark;
	int ivex,jvex;
	struct EBox *ilink, *jlink;
}EBox;
typedef struct VexBox {
	VertexType data;
	EBox *firstedge;
}VexBox;
typedef struct {
	VexBox adjmulist[10];
	int vexnum, edgenum;
}

应用示例

// 邻接表节点
typedef struct AdjListNode {
    int dest; // 目标顶点
    struct AdjListNode* next; // 指向下一个邻接点
} AdjListNode;

// 邻接表头节点
typedef struct AdjList {
    int vertexInfo; // 存储顶点信息
    AdjListNode* head; // 指向第一个邻接点
} AdjList;

// 图结构
typedef struct Graph {
    int V; // 顶点数
    AdjList* array; // 邻接表数组
} Graph;

// 创建邻接表节点
AdjListNode* newAdjListNode(int dest) {
    AdjListNode* newNode = (AdjListNode*)malloc(sizeof(AdjListNode));
    newNode->dest = dest;
    newNode->next = NULL;
    return newNode;
}

// 创建图
Graph* createGraph(int V, int* vertexInfos) {
    Graph* graph = (Graph*)malloc(sizeof(Graph));
    graph->V = V;

    // 创建邻接表数组，并初始化每个链表为空
    graph->array = (AdjList*)malloc(V * sizeof(AdjList));

    for (int i = 0; i < V; ++i) {
        graph->array[i].vertexInfo = vertexInfos[i]; // 存储顶点信息
        graph->array[i].head = NULL;
    }

    return graph;
}

// 添加边到图
void addEdge(Graph* graph, int src, int dest) {
    // 添加从src到dest的边
    AdjListNode* newNode = newAdjListNode(dest);
    newNode->next = graph->array[src].head;
    graph->array[src].head = newNode;
}

// 打印邻接表
void printGraph(Graph* graph) {
    for (int v = 0; v < graph->V; ++v) {
        AdjListNode* pCrawl = graph->array[v].head;
        printf("\n Adjacency list of vertex %d (info: %d)\n head ", v, graph->array[v].vertexInfo);
        while (pCrawl) {
            printf("-> %d", pCrawl->dest);
            pCrawl = pCrawl->next;
        }
        printf("\n");
    }
}


void fun_task_1() {
    int V, E;

    // 输入顶点数和顶点信息
    printf("Enter number of vertices: ");
    scanf("%d", &V);

    int* vertexInfos = (int*)malloc(V * sizeof(int));
    printf("Enter vertex information (e.g., 1 2 3 4 5): ");
    for (int i = 0; i < V; ++i) {
        scanf("%d", &vertexInfos[i]);
    }

    // 输入边数和边信息
    printf("Enter number of edges: ");
    scanf("%d", &E);

    // 创建图
    Graph* graph = createGraph(V, vertexInfos);

    printf("Enter edges (source destination):\n");
    for (int i = 0; i < E; ++i) {
        int src, dest;
        scanf("%d %d", &src, &dest);
        addEdge(graph, src, dest);
    }

    // 输出邻接表
    printGraph(graph);

    // 释放动态分配的内存
    free(vertexInfos);
    for (int i = 0; i < V; ++i) {
        AdjListNode* pCrawl = graph->array[i].head;
        while (pCrawl) {
            AdjListNode* temp = pCrawl;
            pCrawl = pCrawl->next;
            free(temp);
        }
    }
    free(graph->array);
    free(graph);
}

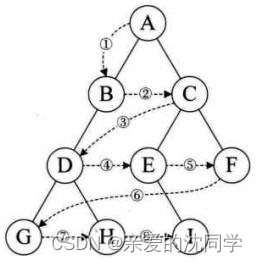
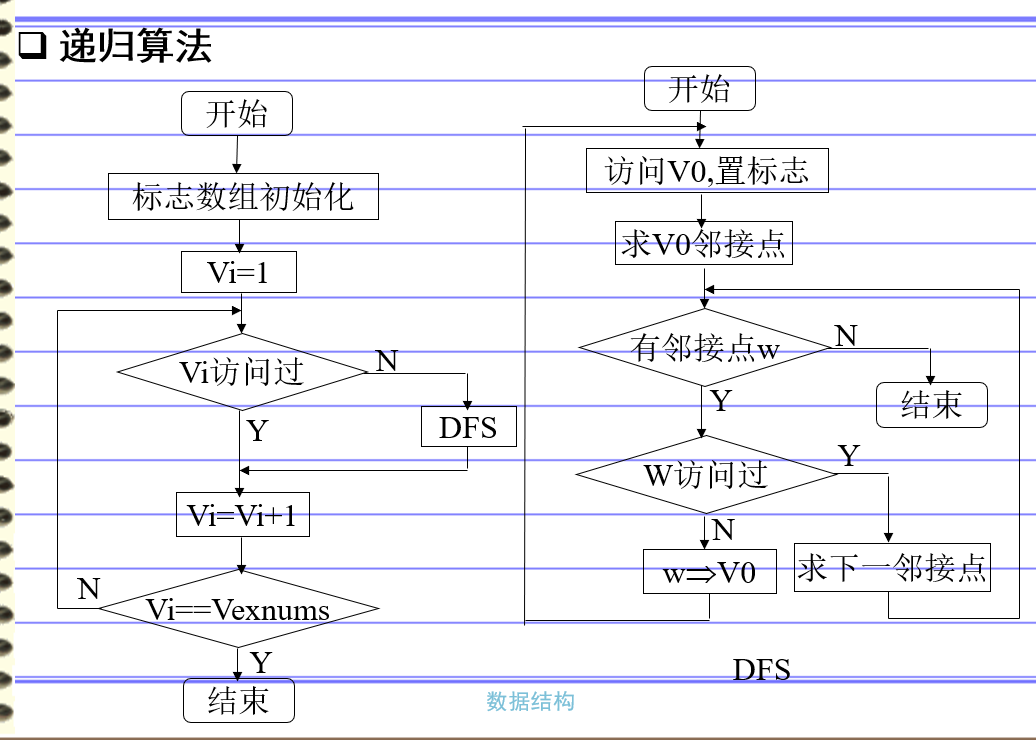
图的遍历

深度优先搜索

如下图，对应于邻接表而言就是这样。

bool visited[MAX_VERTEX_NUM];	//访问标记数组
/*从顶点出发，深度优先遍历图G*/
void DFS(Graph G, int v){
	int w;
	visit(v);	//访问顶点
	visited[v] = TRUE;	//设已访问标记
	//FirstNeighbor(G,v):求图G中顶点v的第一个邻接点，若有则返回顶点号，否则返回-1。
	//NextNeighbor(G,v,w):假设图G中顶点w是顶点v的一个邻接点，返回除w外顶点v
	for(w = FirstNeighbor(G, v); w>=0; w=NextNeighor(G, v, w)){
		if(!visited[w]){	//w为u的尚未访问的邻接顶点
			DFS(G, w);
		}
	}
}
/*对图进行深度优先遍历*/
void DFSTraverse(MGraph G){
	int v; 
	for(v=0; v<G.vexnum; ++v){
		visited[v] = FALSE;	//初始化已访问标记数据
	}
	for(v=0; v<G.vexnum; ++v){	//从v=0开始遍历
		if(!visited[v]){
			DFS(G, v);
		}
	}
}

下面的代码并不是用的上面的流程图。

bool DFSUtil(Graph* graph, int v, int target, bool visited[]) {
    // 标记当前顶点为已访问
    visited[v] = true;

    // 如果找到目标顶点，返回 true
    if (v == target) {
        return true;
    }

    // 遍历当前顶点的所有邻接顶点
    AdjListNode* pCrawl = graph->array[v].head;
    while (pCrawl) {
        int adjVertex = pCrawl->dest;
        if (!visited[adjVertex]) { // 如果邻接顶点未被访问
            if (DFSUtil(graph, adjVertex, target, visited)) {
                return true; // 找到路径
            }
        }
        pCrawl = pCrawl->next;
    }

    return false; // 未找到路径
}

// 判断是否存在从 Vi 到 Vj 的路径
bool isPathExist(Graph* graph, int Vi, int Vj) {
    if (Vi == Vj) {
        return true; // 起点和终点相同，直接返回 true
    }

    // 初始化访问标记数组
    bool* visited = (bool*)malloc(graph->V * sizeof(bool));
    for (int i = 0; i < graph->V; ++i) {
        visited[i] = false;
    }

    // 调用 DFS 辅助函数
    bool result = DFSUtil(graph, Vi, Vj, visited);

    // 释放动态分配的内存
    free(visited);

    return result;
}

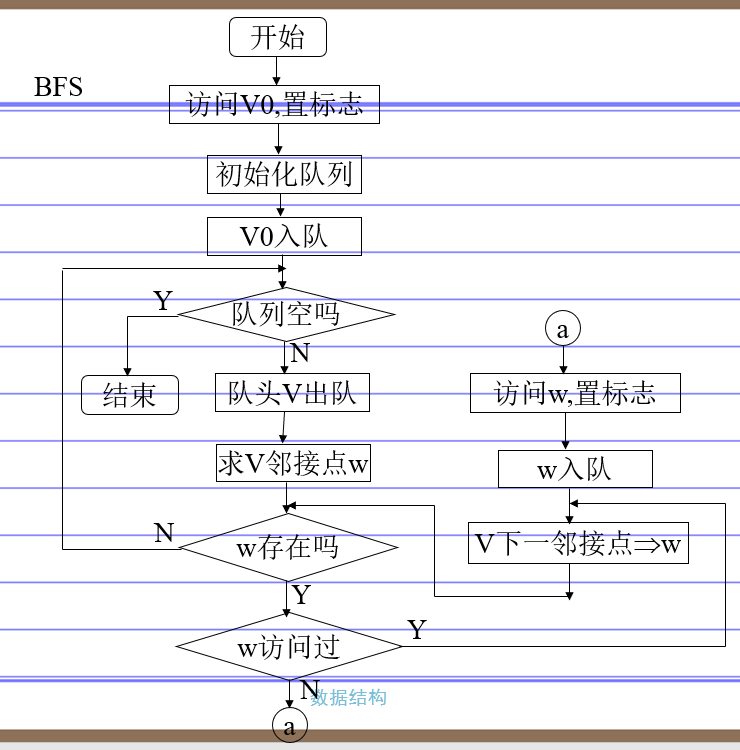
广度优先搜索

/*邻接矩阵的广度遍历算法*/
void BFSTraverse(MGraph G){
	int i, j;
	Queue Q;
	for(i = 0; i<G,numVertexes; i++){
		visited[i] = FALSE;
	}
	InitQueue(&Q);	//初始化一辅助用的队列
	for(i=0; i<G.numVertexes; i++){
		//若是未访问过就处理
		if(!visited[i]){
			vivited[i] = TRUE;	//设置当前访问过
			visit(i);	//访问顶点
			EnQueue(&Q, i);	//将此顶点入队列
			//若当前队列不为空
			while(!QueueEmpty(Q)){
				DeQueue(&Q, &i);	//顶点i出队列
				//FirstNeighbor(G,v):求图G中顶点v的第一个邻接点，若有则返回顶点号，否则返回-1。
				//NextNeighbor(G,v,w):假设图G中顶点w是顶点v的一个邻接点，返回除w外顶点v
				for(j=FirstNeighbor(G, i); j>=0; j=NextNeighbor(G, i, j)){
					//检验i的所有邻接点
					if(!visited[j]){
						visit(j);	//访问顶点j
						visited[j] = TRUE;	//访问标记
						EnQueue(Q, j);	//顶点j入队列
					}
				}
			}
		}
	}
}

其他

比如最小生成树、关键路径等，这里略去

最短路径